TD1

Nous sommes ici en présence d’un système dynamique non linéaire de dimension 4, possédant une unique entrée. En utilisant comme vecteur d’état $X=\transp{\begin{pmatrix}x & \theta & \dot{x} & \dot{\theta}\end{pmatrix}}$ et comme entrée $U=\begin{pmatrix}F\end{pmatrix}$, il vient

Le pendule est à l’équilibre pour tout $X_e = \transp{\begin{pmatrix} xe & 0 & 0 & 0\end{pmatrix}}$

• Les lignes 14 à 19 décrive une classe servant au paramétrage de la fonction de dynamique. m, M, et l sont respectivement la masse du pendule, celle du chariot et la longueur du bras. sat est une saturation optionelle sur l’entrée.

class Param:
    def __init__(self, sat=None):
        self.m     = 0.5     # mass in kg
        self.M     = 0.25    # mass in kg
        self.l     = 1.      # length in m
        self.sat   = sat     # max thrust of motor

• Les lignes 21 à 34 nomment les composantes des vecteurs d’état et d’entrée. code

#
# Components of the state vector
#
sv_x    = 0  # pos of the cg of the cart in m
sv_th   = 1  # orientation of the arm in rad, 0 up
sv_xd   = 2  # velocity of the cart in m/s
sv_thd  = 3  # rotational velocity of the arm in rad/s
sv_size = 4  # dimension of the state vector

#
# Components of the input vector
#
iv_f    = 0  # force on the cart in N
iv_size = 1  # dimension of the input vector

• Les lignes 36 à 61 contiennent la définition de la fonction de dynamique $f$.

#
# Dynamic model as state space representation
#
# X : state
# U : input
# P : param
#
# returns Xd, time derivative of state
#
def dyn(X, t, U, P):

    Xd = np.zeros(sv_size)
    th, thd = X[sv_th], X[sv_thd] 
    sth, cth = np.sin(th), np.cos(th)

    # saturate input
    f = np.clip(U[iv_f], -P.sat, P.sat) if P.sat != None else U[iv_f]
    # upper rows are found directly in state vector
    Xd[sv_x]  = X[sv_xd]
    Xd[sv_th] = thd
    # compute the lower rows
    a = P.M + P.m*(sth**2)
    Xd[sv_xd]  = (f - P.m*P.l*(thd**2)*sth + P.m*9.81*sth*cth) / a
    Xd[sv_thd] = (f*cth - P.m*P.l*(thd**2)*sth*cth +(P.M+P.m)*9.81*sth) / a / P.l
    
    return Xd

La fonction sim_open_loop (lignes 130 à 136) réalise une simulation du pendule sur une durée de 10 secondes, avec un pas de temps de 0.01 secondes avec une entrée nulle et à partir de l’état initial $X_0$

def sim_open_loop(X0):
    P, U = Param(), [0]
    time = np.arange(0., 10, 0.01)
    X = scipy.integrate.odeint(dyn, X0, time, args=(U, P ))
    U = np.zeros((len(time), 1))
    return time, X, U

Les lignes 160 à 164 réalisent la simulation et l’affichent

    time, X, U = sim_open_loop([0, 0, 0, 0.001])
    print('The pendulum is tipping, your job is now to keep it upright')
    plot(time, X, U)
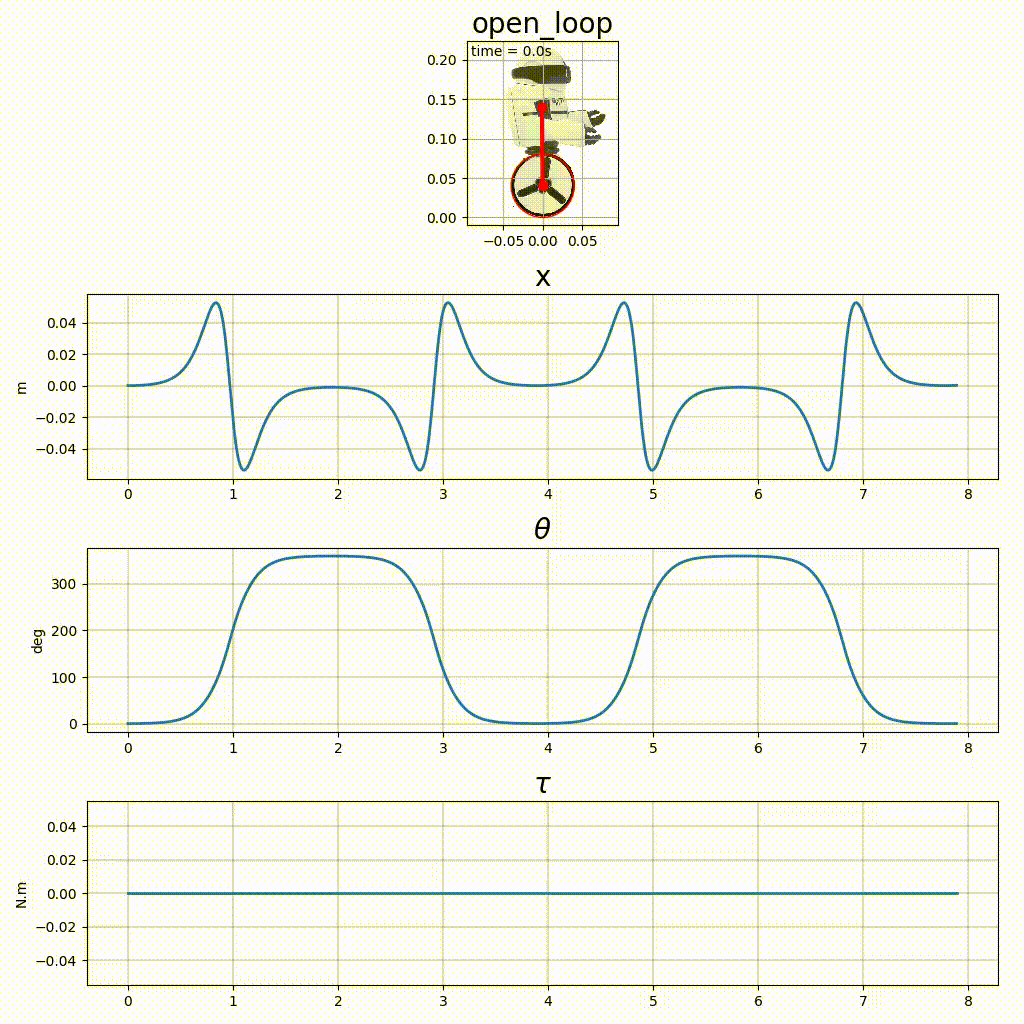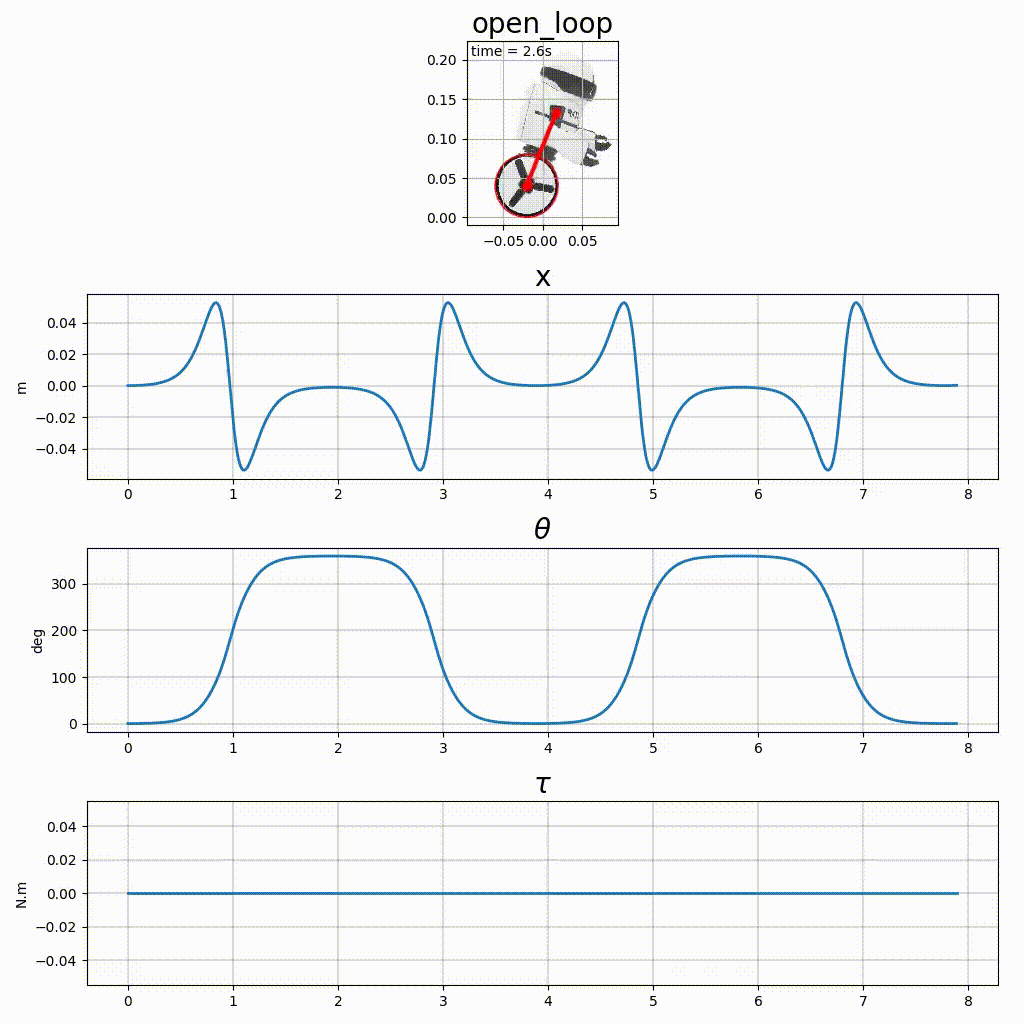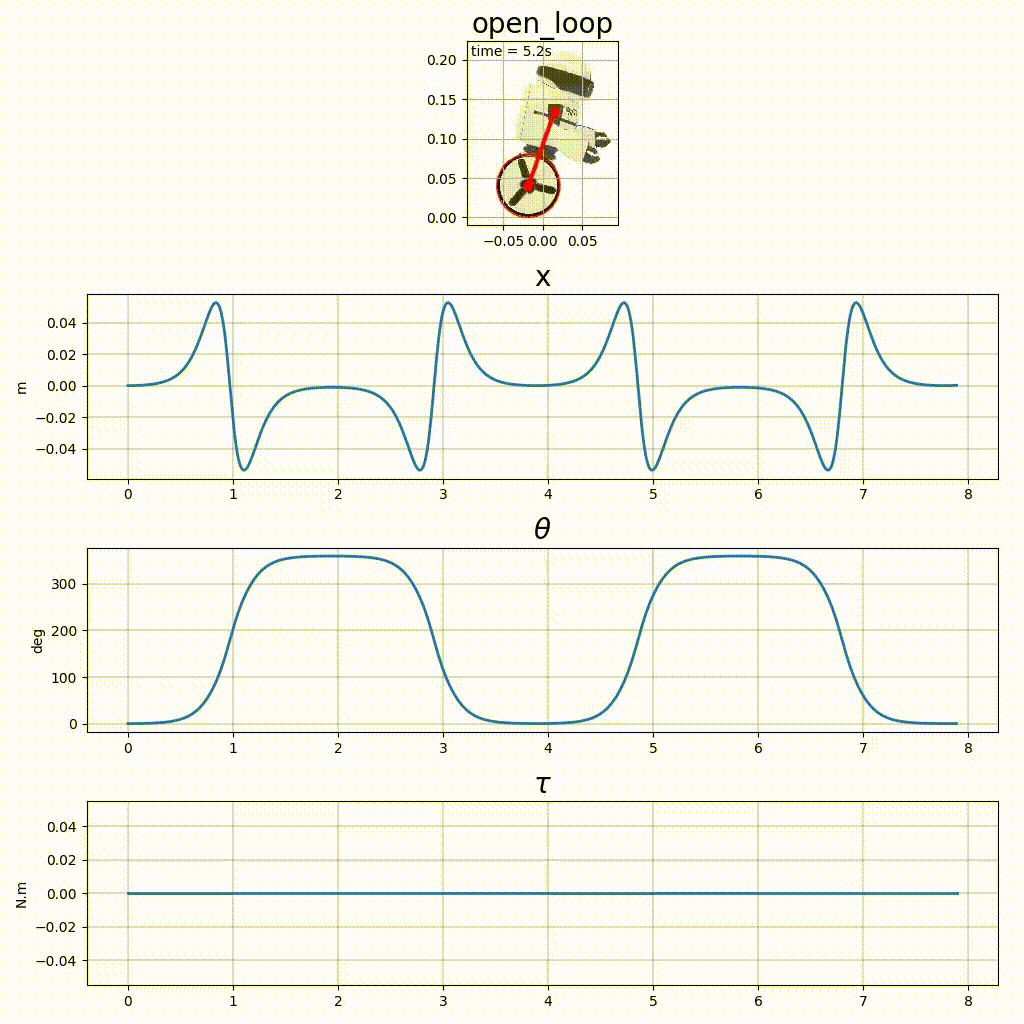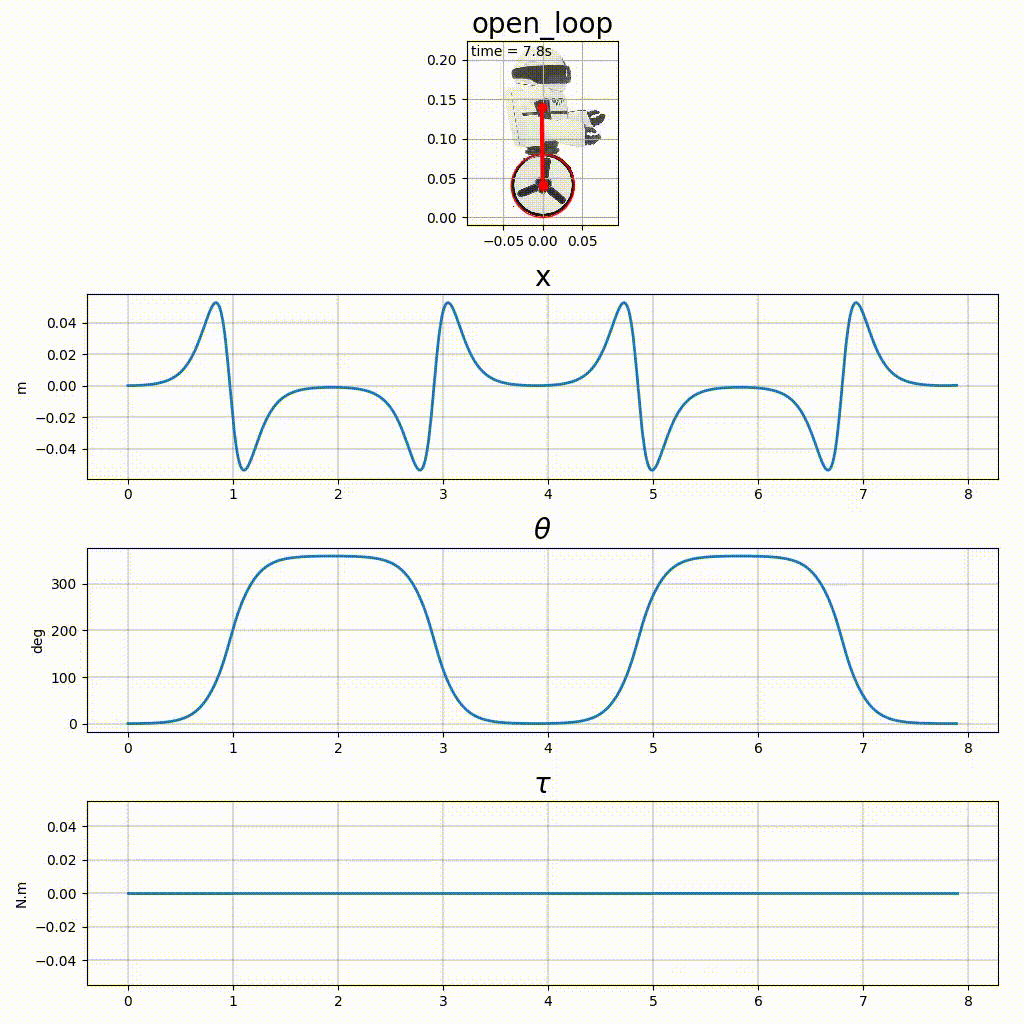
    plt.show()

La figure 2 présente les résultats.

La figure 3, en plus des chronogrammes, présente une animation. Ce type de représentation, intuitive pour l’humain est assez simple à réaliser avec matplotlib.

La représentation d’état linéarisée est

avec

Dans notre cas les jacobiens peuvent etre calculés analytiquement. Le résultat du calcul est présenté dans le squelette de code.

Les lignes 64 à 91 contiennent la définition des jacobiens de la fonction de dynamique (oui, je les ai calculés…). code

#
# (analytic) Jacobians of the Dynamic Model
#
def jacobian(X, U, P):

    th, thd = X[sv_th], X[sv_thd] 
    sth, cth = np.sin(th), np.cos(th)
    v = P.M + P.m*(sth**2)

    A = np.zeros((4,4))
    A[sv_x][sv_xd] = 1.
    A[sv_th][sv_thd] = 1.

    f3num = U[iv_f] - P.m*P.l*(thd**2)*sth + P.m*9.81*sth*cth 
    f3den = P.M + P.m*(sth**2)
    xdd = f3num/f3den
    df3n_dth = -P.m*P.l*(thd**2)*cth + P.m*9.81*(2.*(cth**2)-1.)
    df3d_dth = 2.*P.m*sth*cth
    A[sv_xd][sv_th] = (df3n_dth*f3den-f3num*df3d_dth)/(f3den**2)
    A[sv_xd][sv_thd] = -2*P.m*P.l*thd*sth/f3den
    A[sv_thd][sv_th] = 1./P.l*(9.81*cth + A[sv_xd][sv_th]*cth - xdd*sth)
    A[sv_thd][sv_thd] = cth/P.l*A[sv_xd][sv_thd]

    B = np.zeros((4,1))
    B[sv_xd]  = 1./f3den 
    B[sv_thd] = cth/v/P.l 
    
    return A,B

Lorsqu’un résultat analytique n’est pas disponible, on peut facilement utiliser une differenciation numérique pour approcher les jacobiens (comme cela est aussi présenté dans le squelette de code).

Les lignes 96 à 110 contiennent une version numerique du jacobien (utilisée avant d’obtenir la version analytique). D’autre part, ce calcul numérique peut aussi servir à valider le calcul et l’implémentation de l’expression analytique. code

def num_jacobian(X, U, P):
    dX = np.diag([0.01, 0.01, 0.01, 0.01])
    A = np.zeros((sv_size, sv_size))
    for i in range(0, sv_size):
        dx = dX[i,:]
        delta_f = dyn(X+dx/2, 0, U, P) - dyn(X-dx/2, 0, U, P)
        delta_f = delta_f / dx[i]
        A[:,i] = delta_f

    dU = np.diag([0.01])
    delta_f = dyn(X, 0, U+dU/2, P) - dyn(X, 0, U-dU/2, P)
    delta_f = delta_f / dU
    B = np.zeros((sv_size,iv_size))
    B[:,0] = delta_f
    return A,B

Le calcul des jacobiens pour les paramètres par défaut conduit à

P = Param()
A, B = jacobian([0, 0, 0, 0], [0], P)
print('A\n{}\nB\n{}'.format(A, B))

A
[[ 0.    0.    1.    0.  ]
[ 0.    0.    0.    1.  ]
[ 0.   19.62  0.   -0.  ]
[ 0.   29.43  0.   -0.  ]]
B
[[0.]
[0.]
[4.]
[4.]]

Les strutures propres (valeurs propres, et vecteurs propres) peuvent être obtenus avec:

eig_va, eig_ve =  np.linalg.eig(A)
print(f'pole bo {eig_va}')

pole bo [ 0.         0.         5.4249424 -5.4249424]

Le linéarisé possède un mode à partie réelle positive, il est donc instable. Cela confirne notre intuition (le pendule tombe si on ne fait rien contre) ainsi que la précédente simulation.

La matrice de commandabilité et son rang peuvent être calculés avec

Qc = control.matlab.ctrb(A, B)
print(f'rang Qc {np.linalg.matrix_rank(Qc)}')

Le système est en conséquence complètement commandable. Ceci confirme aussi notre intuition: le monocycle n’est pas une utopie.

cl_poles = [-2, -2.1, -2.2, -2.3]
#K = control.matlab.place(A, B, cl_poles)
K = np.array(control.matlab.acker(A, B, poles)) Vous pouvez vérifier que votre calcul à fonctionné en calculant

print(f'poles bf {np.linalg.eig(A-np.dot(B, K))[0]}')

Le squelette de code contient une fonction permettant la simulation du pendule et de son correcteur, sim_state_feedback.

def sim_state_feedback(X0, K):
    P = Param()
    def cl_dyn(X, t): return dyn(X, t, [-np.dot(K, X)], P)
    time = np.arange(0., 10, 0.01)
    X = scipy.integrate.odeint(cl_dyn, X0, time)
    U =  np.array([[-np.dot(K, Xi)] for Xi in X])
    return time, X, U

Vous constaterez sans doute que le pendule tombe à partir d’une certaine valeur de la perturbation.